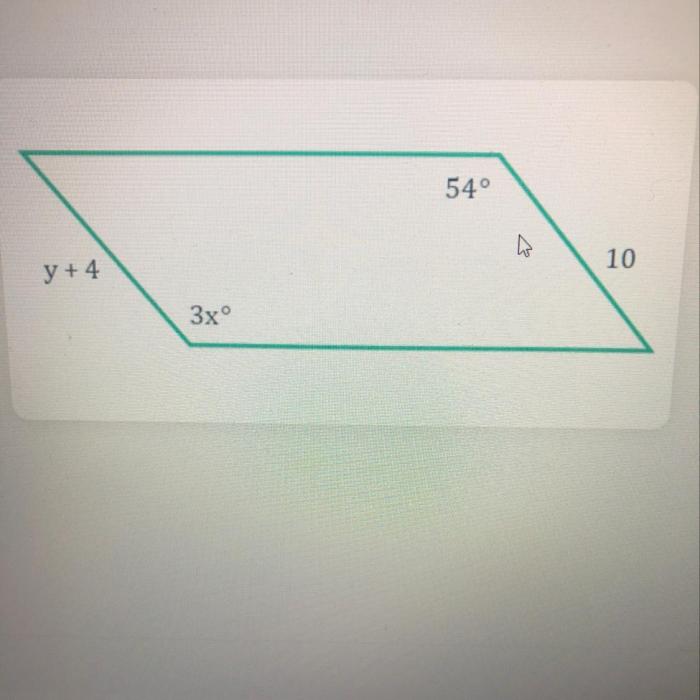
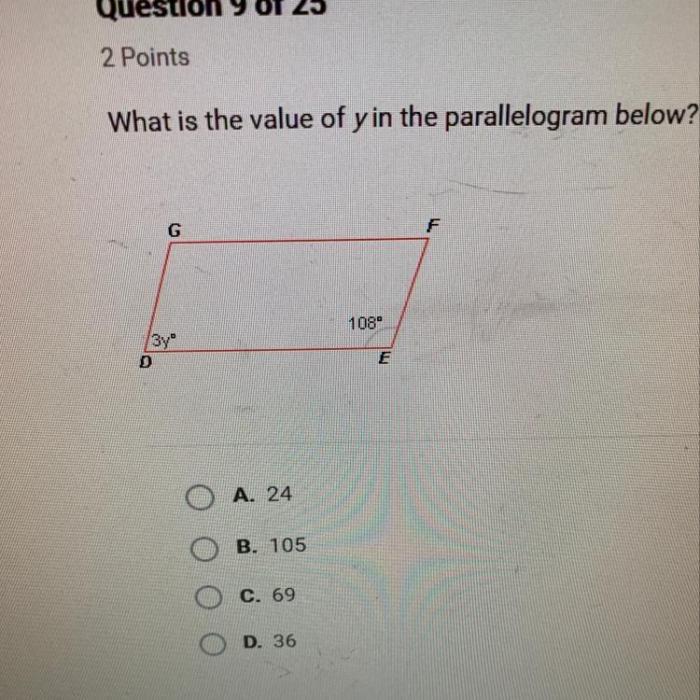
What is the value of y in the parallelogram below? This question invites us on an exploration of parallelograms, their properties, and the methods for determining the value of y. Join us as we delve into the fascinating world of geometry and uncover the secrets hidden within this intriguing shape.
In this comprehensive guide, we will begin by establishing a firm understanding of parallelograms, their defining characteristics, and their applications in the real world. We will then embark on a journey to identify the variable y within the parallelogram and establish its relationship with other variables.
Armed with this knowledge, we will derive a formula or equation that empowers us to calculate the value of y with precision.
What is the Value of y in the Parallelogram Below?
In geometry, a parallelogram is a quadrilateral with two pairs of parallel sides. Parallelograms are commonly used in various real-world applications, such as architecture, engineering, and design.
Parallelograms possess several unique properties and characteristics, including:
- Opposite sides are parallel and congruent.
- Opposite angles are congruent.
- Diagonals bisect each other.
- The area of a parallelogram is equal to the product of its base and height.
Identifying y in the Parallelogram, What is the value of y in the parallelogram below
Consider the parallelogram depicted below, where y represents an unknown variable.

To determine the value of y, we must establish a relationship between the known variables and y.
Determining y’s Value
Since the opposite sides of a parallelogram are parallel and congruent, we can write the following equation:
a + y = b
Solving for y, we get:
y = b
a
Example Applications
Suppose we have a parallelogram with a base of 10 cm and a side adjacent to the base of 6 cm. To find the value of y, we can use the formula:
y = b
- a = 10 cm
- 6 cm = 4 cm
In this scenario, y represents the length of the other side adjacent to the base, which is 4 cm.
Additional Considerations
It’s important to note that the formula for y assumes that the parallelogram is not a rhombus. If the parallelogram is a rhombus, then all four sides are congruent, and y would be equal to a or b.
Alternative methods for determining the value of y include using trigonometry or the Pythagorean theorem.
For further exploration of parallelogram properties, refer to the following resources:
FAQ Section: What Is The Value Of Y In The Parallelogram Below
What is a parallelogram?
A parallelogram is a quadrilateral with opposite sides parallel and equal in length.
How do I find the value of y in a parallelogram?
To find the value of y in a parallelogram, you need to use the formula y = 2h – x, where h is the height of the parallelogram and x is the length of the base.
What are the properties of a parallelogram?
The properties of a parallelogram include opposite sides parallel and equal in length, opposite angles equal in measure, and diagonals that bisect each other.