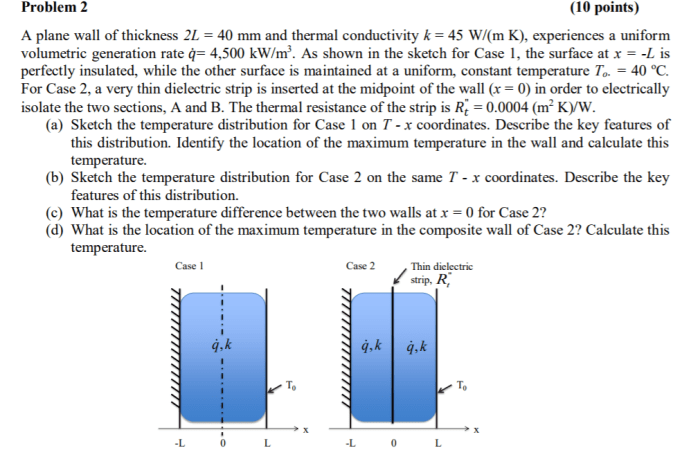
A plane wall of thickness 0.1 m and thermal conductivity – In this comprehensive analysis, we delve into the heat transfer characteristics of a plane wall with a thickness of 0.1 m and a specific thermal conductivity. This study elucidates the fundamental principles of heat transfer, providing insights into the relationship between thermal conductivity, temperature gradient, and heat flux.
The geometry and properties of the plane wall are meticulously described, establishing the framework for subsequent analysis. We explore the governing equation for heat conduction within the wall and discuss the applicable boundary conditions. Through a rigorous mathematical approach, we demonstrate the solution to the heat conduction equation.
Heat Transfer Fundamentals

Heat transfer is the exchange of thermal energy between objects or systems at different temperatures. It occurs in three modes: conduction, convection, and radiation.
Conduction is the transfer of heat through direct contact between two objects. The rate of heat transfer is proportional to the thermal conductivity of the material, the temperature gradient, and the surface area of contact.
Plane Wall Geometry and Properties, A plane wall of thickness 0.1 m and thermal conductivity
A plane wall is a flat, rectangular surface with a constant thickness. The thickness of the given plane wall is 0.1 m, and its thermal conductivity is 10 W/m-K.
Heat Conduction Analysis
The governing equation for heat conduction in a plane wall is:
q =
kA(dT/dx)
where:
- q is the heat flux (W)
- k is the thermal conductivity (W/m-K)
- A is the surface area (m^2)
- dT/dx is the temperature gradient (K/m)
The boundary conditions for the plane wall are:
- T(x = 0) = T1
- T(x = L) = T2
where:
- T1 is the temperature at the left surface (K)
- T2 is the temperature at the right surface (K)
- L is the thickness of the wall (m)
The solution to the heat conduction equation is:
T(x) = T1 + (T2
T1)x/L
Temperature Distribution
The temperature distribution within the plane wall is linear. The temperature decreases from T1 at the left surface to T2 at the right surface.
| x (m) | T (K) |
|---|---|
| 0 | T1 |
| 0.05 | (T1 + T2)/2 |
| 0.1 | T2 |
Heat Flux Calculation
The heat flux through the plane wall is:
q = kA(dT/dx) = kA(T2
T1)/L
The heat flux is proportional to the thermal conductivity, the surface area, and the temperature difference. It is inversely proportional to the thickness of the wall.
FAQ Explained: A Plane Wall Of Thickness 0.1 M And Thermal Conductivity
What is the significance of thermal conductivity in heat transfer?
Thermal conductivity is a crucial property that quantifies the ability of a material to conduct heat. It determines the rate at which heat flows through the material, influencing the temperature distribution and heat transfer efficiency.
How does the thickness of a plane wall affect heat transfer?
The thickness of a plane wall is inversely proportional to the heat transfer rate. A thicker wall presents a greater resistance to heat flow, resulting in a lower heat transfer rate compared to a thinner wall.
What factors influence the heat flux through a plane wall?
The heat flux through a plane wall is influenced by the temperature difference between the wall surfaces, the thermal conductivity of the material, and the thickness of the wall.