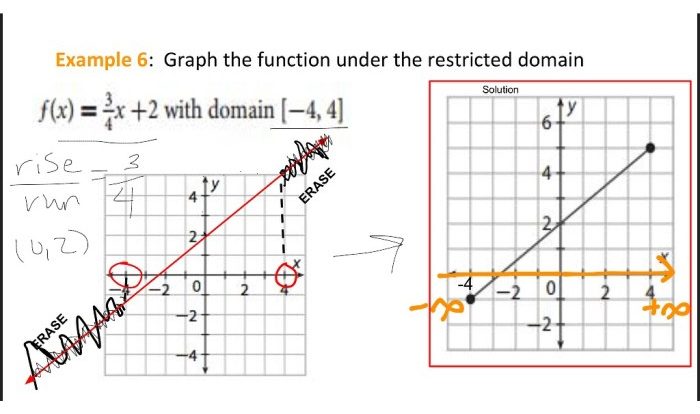
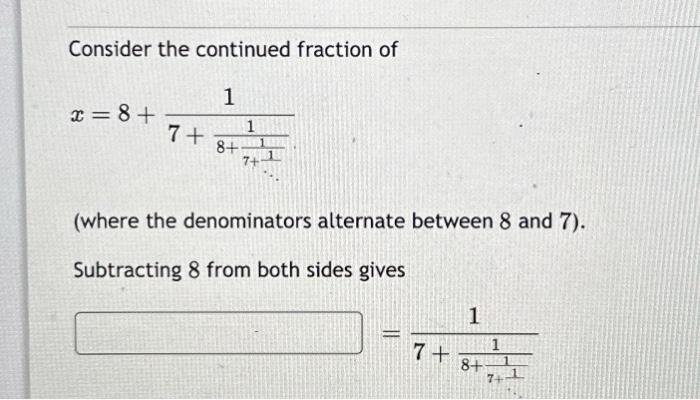
Unit 7 right triangles and trigonometry answers – Welcome to the realm of Unit 7: Right Triangles and Trigonometry, where we delve into the fascinating world of triangles and their enigmatic trigonometric ratios. This comprehensive guide will unravel the mysteries of right triangles, empowering you with the knowledge and skills to conquer any trigonometry challenge.
Throughout this journey, we will explore the fundamental concepts of right triangles, their properties, and the pivotal Pythagorean theorem. We will then venture into the realm of trigonometric ratios, defining sine, cosine, and tangent, and mastering their calculation using right triangles.
With a solid foundation in place, we will embark on the thrilling task of solving right triangles, uncovering step-by-step strategies for finding missing sides and angles.
Right Triangle Basics

Right triangles are triangles with one right angle (90 degrees). They have unique properties that make them useful in various applications. The Pythagorean theorem, which states that the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides, is a fundamental theorem in right triangle geometry.
Real-World Applications of Right Triangles
- Architecture: Determining the height of buildings or the length of beams
- Engineering: Calculating the forces acting on bridges or the stability of structures
- Surveying: Measuring distances and angles in land surveys
Trigonometric Ratios

Trigonometric ratios are functions that relate the lengths of the sides of a right triangle to the angles. The three main trigonometric ratios are sine, cosine, and tangent.
Calculating Trigonometric Ratios
- Sine (sin) = opposite side / hypotenuse
- Cosine (cos) = adjacent side / hypotenuse
- Tangent (tan) = opposite side / adjacent side
These ratios can be used to solve right triangles when given certain information.
Table of Trigonometric Ratios for Special Angles
| Angle | Sine | Cosine | Tangent |
|---|---|---|---|
| 0° | 0 | 1 | 0 |
| 30° | 1/2 | √3/2 | 1/√3 |
| 45° | √2/2 | √2/2 | 1 |
| 60° | √3/2 | 1/2 | √3 |
| 90° | 1 | 0 | undefined |
Solving Right Triangles
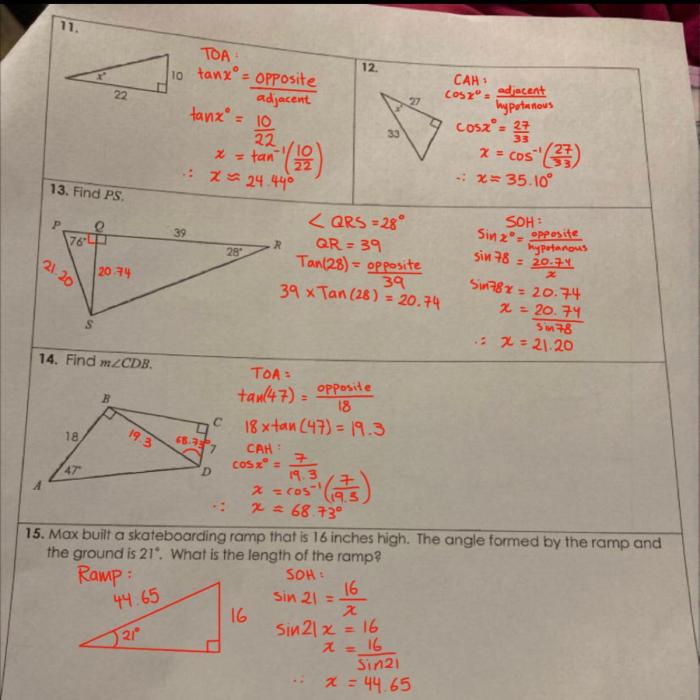
Trigonometric ratios can be used to solve right triangles by finding missing sides or angles. The process involves using the given information to set up equations and solve for the unknown values.
Steps for Solving Right Triangles
- Identify the given information and the unknown value(s).
- Choose the appropriate trigonometric ratio based on the given information.
- Set up an equation using the trigonometric ratio.
- Solve the equation for the unknown value(s).
Applications of Right Triangle Trigonometry, Unit 7 right triangles and trigonometry answers
- Surveying: Determining the height of objects or the distance between two points
- Navigation: Calculating the course and distance of a ship or aircraft
- Astronomy: Measuring the distances to stars and other celestial objects
Applications of Trigonometry: Unit 7 Right Triangles And Trigonometry Answers
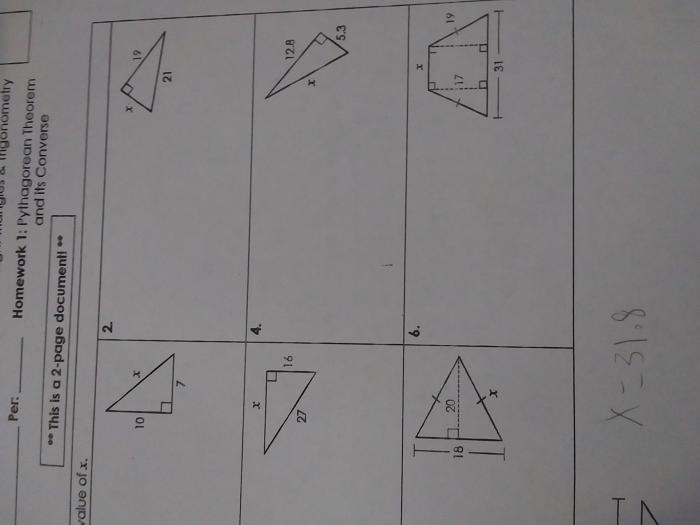
Trigonometry is a powerful tool used in a wide range of fields beyond right triangle solving. Its principles are applied in engineering, architecture, astronomy, and many other disciplines.
Examples of Trigonometry Applications
- Engineering: Designing bridges, buildings, and other structures
- Architecture: Calculating the angles of roofs and the heights of buildings
- Astronomy: Measuring the distances to stars and planets, and determining the trajectories of celestial objects
Trigonometry plays a vital role in modern technology and innovation, enabling us to solve complex problems and make advancements in various fields.
FAQ Compilation
What is the Pythagorean theorem?
The Pythagorean theorem states that in a right triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides.
How do I calculate trigonometric ratios?
Trigonometric ratios are calculated using the ratios of the sides of a right triangle. Sine is opposite/hypotenuse, cosine is adjacent/hypotenuse, and tangent is opposite/adjacent.
How do I solve right triangles?
Right triangles can be solved using trigonometric ratios and the Pythagorean theorem. By knowing the length of two sides or an angle, you can find the missing sides or angles.