Points of concurrency of a triangle – Points of concurrency in triangles, where lines and segments meet, play a pivotal role in triangle geometry. This discourse delves into their significance, uncovering their types, constructions, properties, and applications.
From angle bisectors to medians and altitudes, points of concurrency serve as geometric landmarks, guiding us through the intricate world of triangles.
Points of Concurrency of a Triangle
In triangle geometry, points of concurrency are special points where multiple lines or segments intersect. These points play a significant role in understanding and analyzing triangle properties.
Types of Points of Concurrency
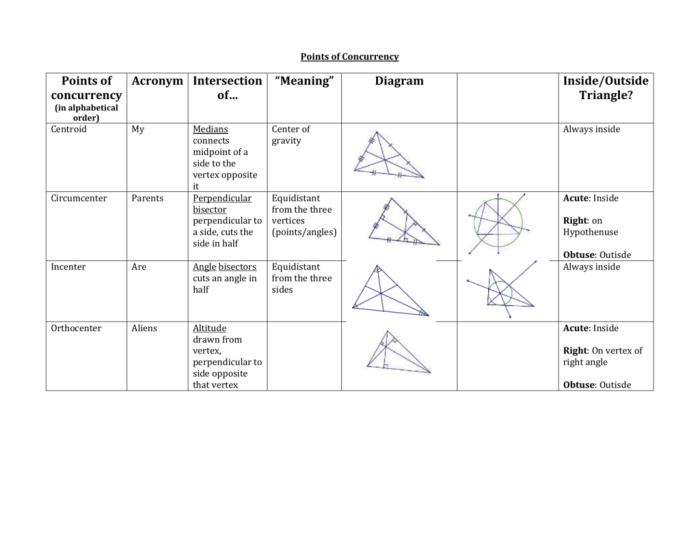
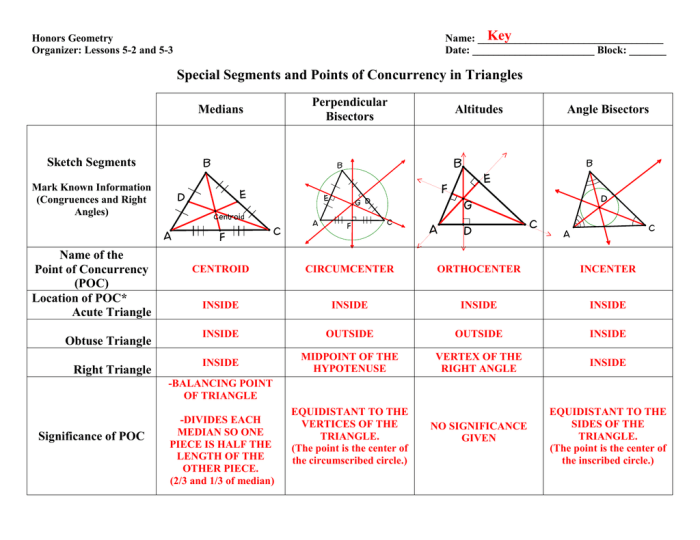
- Incenter:The point of intersection of the angle bisectors of a triangle.
- Circumcenter:The point of intersection of the perpendicular bisectors of the sides of a triangle.
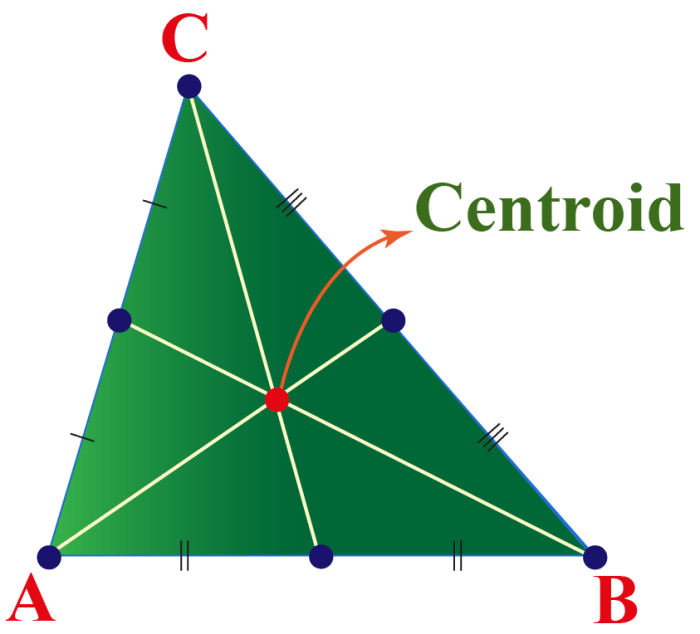
- Centroid:The point of intersection of the medians of a triangle.
- Orthocenter:The point of intersection of the altitudes of a triangle.
Constructions of Points of Concurrency, Points of concurrency of a triangle
Incenter:Construct the angle bisectors of each angle and locate their point of intersection.
Circumcenter:Construct the perpendicular bisectors of each side and locate their point of intersection.
Centroid:Divide each median into three equal parts and locate the point of intersection of the two smaller parts.
Orthocenter:Construct the altitudes from each vertex and locate their point of intersection.
Properties of Points of Concurrency
- The incenter is equidistant from the three sides of a triangle.
- The circumcenter is equidistant from the three vertices of a triangle.
- The centroid divides each median into a ratio of 2:1.
- The orthocenter lies outside the triangle if it is acute, on the hypotenuse if it is right-angled, and inside the triangle if it is obtuse.
Applications of Points of Concurrency
- Solving geometric problems involving angle bisectors, medians, and altitudes.
- Determining the center of a circle inscribed in or circumscribed about a triangle.
- Finding the orthocenter of a triangle to determine whether it is acute, right-angled, or obtuse.
Historical Development of Points of Concurrency
The concept of points of concurrency has been studied since ancient times. Greek mathematicians, such as Euclid and Archimedes, investigated these points and their properties. In the 17th century, René Descartes developed analytic geometry, which provided a systematic framework for studying points of concurrency.
FAQ Insights: Points Of Concurrency Of A Triangle
What are points of concurrency in triangles?
Points of concurrency are special points in a triangle where multiple lines or segments intersect.
What are the different types of points of concurrency?
There are several types of points of concurrency, including the centroid, circumcenter, incenter, and orthocenter.
How are points of concurrency constructed?
Points of concurrency can be constructed using various methods, such as angle bisectors, medians, and altitudes.
What are the properties of points of concurrency?
Points of concurrency possess unique geometric properties, such as being equidistant from the vertices or lying on perpendicular bisectors.
What are the applications of points of concurrency?
Points of concurrency are used in solving geometric problems, such as finding the area or centroid of a triangle.